Les traductions sont fournies par des outils de traduction automatique. En cas de conflit entre le contenu d'une traduction et celui de la version originale en anglais, la version anglaise prévaudra.
Valeurs de Shapley asymétriques
La solution d'explication du modèle de prévision des séries chronologiques SageMaker Clarify est une méthode d'attribution de fonctionnalités ancrée dans la théorie des jeux coopératifs
Contexte
L’objectif est de calculer les attributions des caractéristiques d’entrée pour un modèle de prévision donné f. Le modèle de prévision accepte les entrées suivantes :
Séries temporelles passées (TS cible). Par exemple, il peut s’agir d’anciens passagers quotidiens sur le trajet Paris-Berlin, indiqués par xt.
(Facultatif) Une série temporelle à covariables. Par exemple, il peut s’agir de fêtes et de données météorologiques, désignées par zt ∈ RS. Lorsqu’elle est utilisée, la covariable TS peut être disponible uniquement pour les étapes temporelles passées ou également pour les étapes futures (incluses dans le calendrier des fêtes).
(Facultatif) Covariables statiques, telles que la qualité de service (comme la première ou la deuxième classe), désignée par u ∈ RE.
Les covariables statiques, les covariables dynamiques ou les deux peuvent être omises, selon le scénario d’application spécifique. Étant donné un horizon de prédiction K ≥ 0 (p. ex., K=30 jours), la prédiction modélisée peut être caractérisée par la formule : f(x[1:T], z[1:T+K], u) = x[T+1:T +K+1].
Le schéma suivant illustre une structure de dépendance pour un modèle de prévision classique. La prédiction à l’instant t+1 dépend des trois types d’entrées mentionnés précédemment.
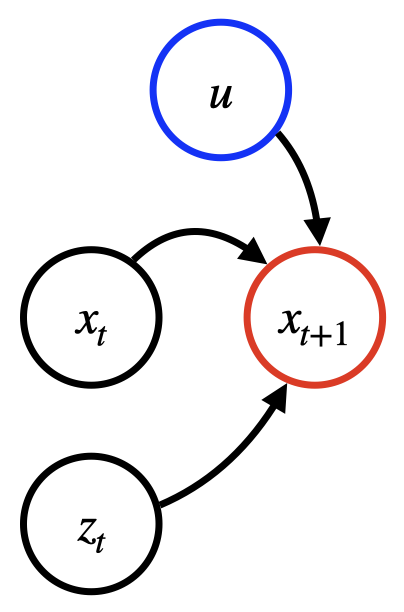
Method
Les explications sont calculées en interrogeant le modèle de série temporelle f sur une série de points dérivés de l’entrée d’origine. En suivant les constructions de la théorie des jeux, Clarify fait la moyenne des différences entre les prédictions par obfuscation (c’est-à-dire en fixant à une valeur de référence) de certaines parties des entrées de manière itérative. La structure temporelle peut être parcourue dans un ordre chronologique, antichronologique ou les deux. Les explications chronologiques sont élaborées en ajoutant de manière itérative des informations à partir de la première étape temporelle, tandis que les explications antichronologiques sont élaborées à partir de la dernière étape. Ce dernier mode peut être plus approprié en présence d’un biais de récence, par exemple lors de la prévision du cours des actions. Une propriété importante des explications calculées est que leur somme correspond à la sortie du modèle d’origine si le modèle fournit des sorties déterministes.
Attributions résultantes
Les attributions résultantes sont des scores qui indiquent les contributions individuelles d’étapes temporelles spécifiques ou de caractéristiques d’entrée spécifiques envers la prévision finale à chaque étape temporelle prévue. Clarify propose les deux granularités suivantes pour les explications :
Les explications temporelles sont peu coûteuses et fournissent uniquement des informations sur des étapes temporelles spécifiques, telles que la mesure dans laquelle les informations du 19e jour dans le passé ont contribué à la prévision du 1er jour dans le futur. Ces attributions n’expliquent pas les covariables statiques individuelles ni les explications agrégées des séries temporelles cibles et à covariables. Les attributions sont une matrice A où chaque Atk est l’attribution de l’étape temporelle t envers la prévision de l’étape temporelle T+k. Notez que si le modèle accepte les covariables futures, t peut être supérieur à T.
Les explications précises sont plus gourmandes en calculs et fournissent une ventilation complète de toutes les attributions des variables d’entrée.
Note
Les explications précises prennent en charge uniquement l’ordre chronologique.
Les attributions résultantes sont un triplet composé des éléments suivants :
Matrice Ax ∈ RT×K associée à la série temporelle d’entrée, où Atkx est l’attribution de xt envers la prévision de l’étape T+k
Tenseur Az ∈ RT+K×S×K associé à la série temporelle à covariables, où Atskz est l’attribution de zts (c’est-à-dire la s-ième covariable TS) envers la prévision de l’étape T+k
Matrice Au ∈ RE×K associée aux covariables statiques, où Aeku est l’attribution de ue (la e-ième covariable statique) envers la prévision de l’étape T+k
Quelle que soit la granularité, l’explication contient également un vecteur de décalage B ∈ RK qui représente le « comportement élémentaire » du modèle quand toutes les données sont obfusquées.